CommunicatingIntent and Formal Specifications
Marcell J. Vazquez-Chanlatte
Qualifying Exam (March 20th, 2019)
Link to slides: mjvc.me/quals
Motivation: Robot-Human Interaction
Human-Robot interactions are becoming increasingly ubiquitous.

-
Many tasks implicitly require inferring
objectives of other agents.

Cars interacting w. pedestriansIllustration: Bryan Christie Design 
Uber Crash(Photo: FRESCO NEWS/Mark Beach) - Success = Increased need for safety, correctness, and audit-ability.
- Can we leverage formal methods in these domains?
Formal Methods 101
- Formal Verification: Given a specification and a system model, check if the system satisfies the specification.
An Inconvenient Truth
- Formal Verification: Given a specification and a system model, check if the system satisfies the specification.
- Specifications are almost never written down, let alone the "specifications" of human agents.
Specification Mining
- Formal Verification: Given a specification and a system model, check if the system satisfies the specification.
- Specifications are almost never written down, let alone the "specifications" of human agents.
- Specification Mining seeks to fill this void but has largely ignored unlabeled and probabilistic demonstrations.
Exceptions concurrently developed: (Kasenberg et al CDC 2017), (Shah et al NeurIPS 2018)
What are Demonstrations?
- A demonstration of a task is an unlabeled example where the agent tries to perform the task (will revisit definition).
- Agency is key. Need a notion of action.
Demonstrations - Necessary but not sufficient
But why demonstrations vs natural language, etc?
- Natural language is ambiguous.
- People might not mean what they say.
- Demonstrations can be incredibly diagnostic.
- Demonstrations can be used to teach human.
Research Goal
Through my research I seek to develop theory and tools for communicating$^*$ formal specifications.
$^*$: Terminology due to deep connection with Information Theory.
This talk will focus on learning and teaching specifications via demonstrations.
Research Landscape and Current Contributions
- Talk focuses on (NeurIPS 2018).Maximum Entropy IRL (Ziebart, et al. 2008) $\to$ Specification Mining.
- Preliminary work on specification teaching and communication discusses at the end. (CPHS 2018)
- Occasionally you might see links which lead to longer derivations or other research/asides which can supplement the talk.
Structure of the talk
Prelude
Act 1 - Learning Specifications
- Formal Specification Propaganda
- Maximum Entropy Specification Learning (NeurIPS 2018, current work)
Act 2 - Teaching Specifications
- Episodic Specification Teaching (CPHS 2018, future work)
- Cooperative Planningfuture work
- Legibilityfuture work
Act 3 - Challenge Problems
Simplifying Assumptions


- Above domains are currently aspirations.
- 90% of this talk we will focus on
episodic learning (and teaching) with a
single agent.
- Final 10% will treat inter-episodic learning (and teaching) with multiple-agents.
Running Example


High Level Motion Planner
Running Example


High Level Motion Planner
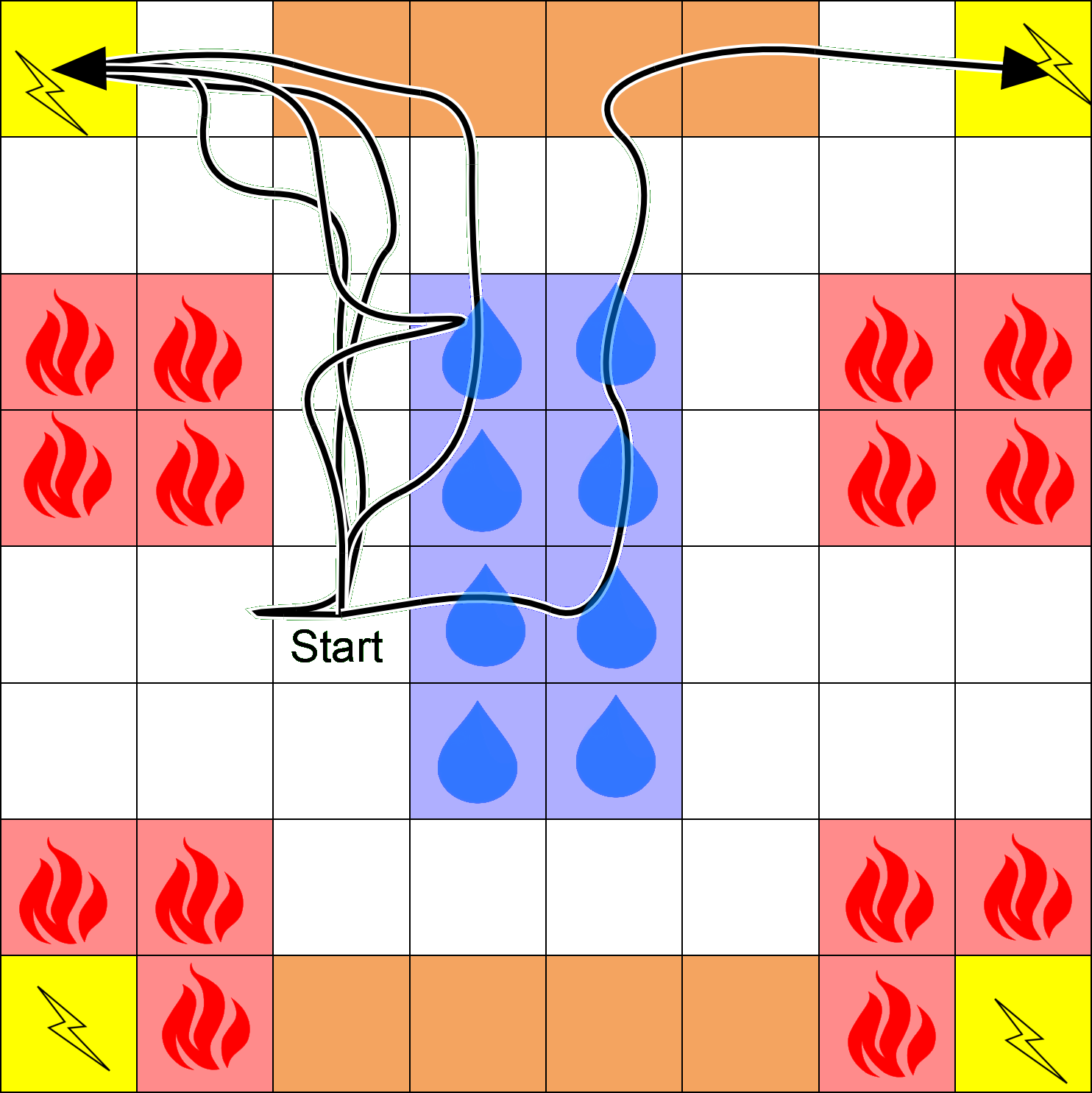
- Dynamics: Can move North, South, East, and West, but may probabilistically slip or be pushed by wind.
- States: In a addition to position, four types of states: lava, water, drying, and recharge.
- The dynamics are independent of the state type.
- Example Task: Eventually recharge while avoiding Lava. If agent enters water, the agent must dry off before recharging.
Structure of the talk
Prelude
Act 1 - Learning Specifications
- Formal Specification Propaganda
- Maximum Entropy Specification Learning (NeurIPS 2018, current work)
Act 2 - Teaching Specifications
- Episodic Specification Teaching (CPHS 2018, future work)
- Cooperative Planningfuture work
Act 3 - Challenge Problems
Basic definitions
-
Assume some fixed set $S$, called states.
- A trace, $\xi$, is a sequence of states.
- A specification(trace property), $\varphi$, is a set of traces.
- We say $\xi$ satisfies $\varphi$, written $\xi \models \varphi$, if $\xi \in \varphi$.
Communicating Intent and Formal Specifications
- Specification: What qualifies as acceptable behavior?
- Derived from Formal Logic, Automata, Rewards ($\epsilon$-"optimal").
-
No a-priori ordering between acceptable behaviors.
- Key question: How to compose specifications. $\circ : $ Specification $\times$ Specification $\to$ Specification
Communicating Intent and Formal Specifications
Key question: How to compose specifications. $\circ : $ Specification $\times$ Specification $\to$ Specification
- Build up complex specifications from simpler ones.
- Can always compose as concrete the sets:
- Preferable to compose at abstract level: $(\neg a \wedge b)$
- Question: How can one compose rewards?
Utility Maximizing Agents
Assume agent is acting in a Markov Decision process and optimizing the sum of an unknown state reward, $r(s)$, i.e,: \[ \begin{split} &\pi : S \times A \to [0, 1]\\ \max_{\pi} &\Big(\mathbb{E}_{s_{1:T}}\big(\sum_{i=1}^T r(s_i)~|~\pi\big)\Big) \end{split} \]
- Agent model reinforcement learning (and optimal control) (Witten 1977, Sutton and Barto 1981)(Bellman 1957).
-
Implicit specification: Pick a trace with (approximately) optimal reward.
Inverse Reinforcement Learning
Assume agent is acting in a Markov Decision process and optimizing the sum of an unknown state reward, $r(s)$, i.e,: \[ \max_{\pi} \Big(\mathbb{E}_{s_{1:T}}\big(\sum_{i=1}^T r(s_i)~|~\pi\big)\Big) \] Given a series of demonstrations, what reward, $r(s)$, best explains the behavior? (Abbeel and Ng 2004)
Will revisit solution techniques.
Problems with rewards
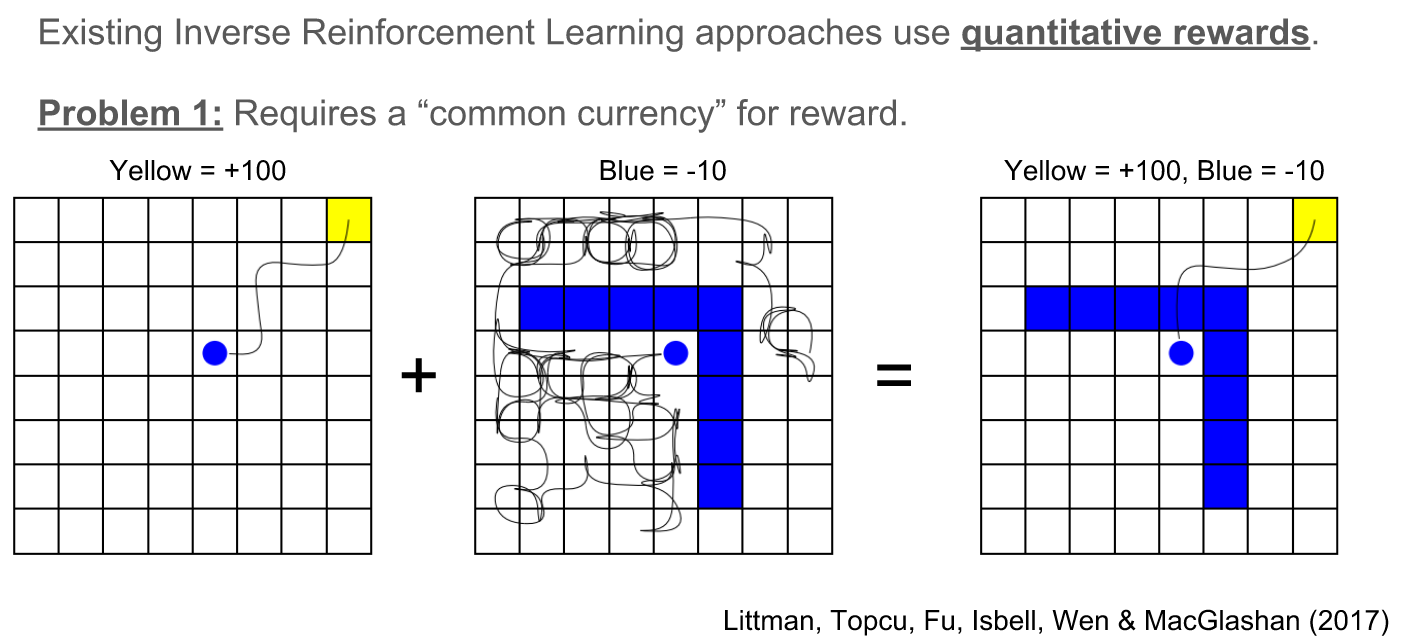
How to safely compose in a dynamics invariant way?
Problems with rewards
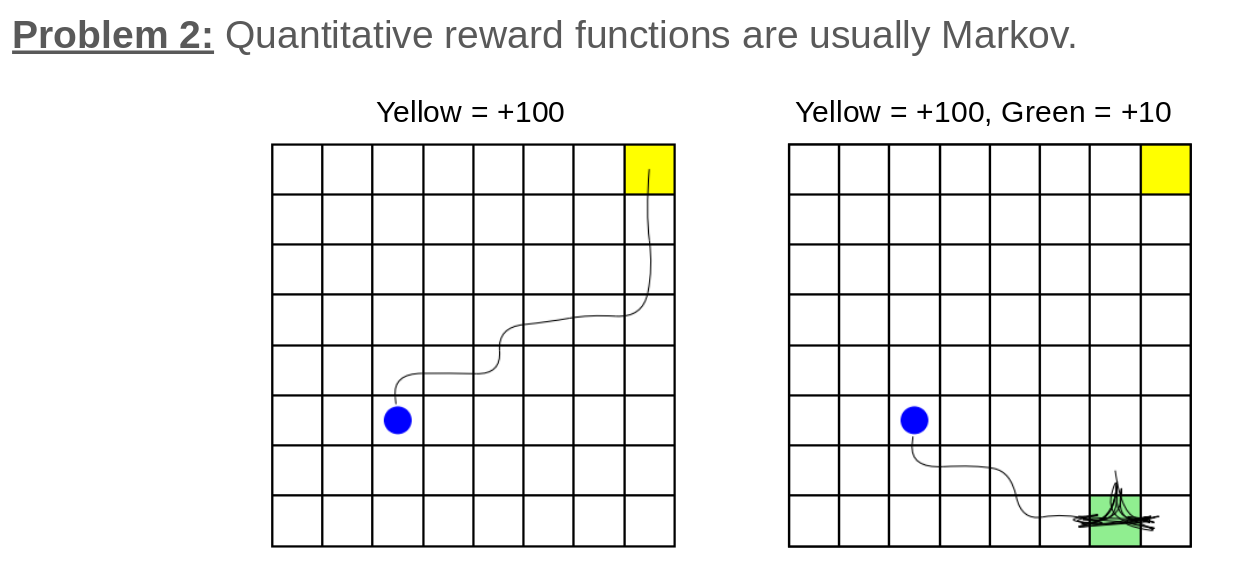
- Dynamic States != Reward States
- Beware the curse of history (Pineau et al 2003). Adding history can result in exponential state space explosion.
Running Example is Compositional and non-Markovian

Example Task
\[ \varphi = \varphi_1 \wedge \varphi_2 \wedge \varphi_3 \]
- $\varphi_1$ = Eventually recharge.
- $\varphi_2$ = Avoid lava.
- $\varphi_3$ = If agent enters water, the agent must dry off before recharging.
Structure of the talk
Prelude
Act 1 - Learning Specifications
- Formal Specification Propaganda
- Maximum Entropy Specification Learning (NeurIPS 2018, current work)
Act 2 - Teaching Specifications
- Episodic Specification Teaching (CPHS 2018, future work)
- Cooperative Planningfuture work
Act 3 - Challenge Problems
Learning Trace Properties from Demonstrations
- A demonstration of a task $\varphi$ is an unlabeled example where the agent tries to satisfy $\varphi$.
- Agency is key. Need a notion of action.
-
Success probabilities induce an ordering.
Informal Problem Statement
- Assume an agent is operating in a Markov Decision Process while trying to satisfy some unknown specification.
- Given a sequence of demonstrations, $\text{demos}$, and a collection of specifications, $\Phi$, find the specification $\varphi \in \Phi$ that best explains the agent's behavior.
Idea: Apply analog to Inverse Reinforcement Learning.
Inverse Reinforcement Learning
Assume agent is acting in a Markov Decision process and optimizing the sum of an unknown state reward, $r(s)$, i.e,: \[ \max_{\pi} \Big(\mathbb{E}_{s_{1:T}}\big(\sum_{i=1}^T r(s_i)~|~\pi\big)\Big) \] Given a series of demonstrations, what reward, $r(s)$, best explains the behavior? (Abbeel and Ng 2004)
- Note: There is no unique solution as posed! \[ \Pr(\xi~|~\text{demos}, r) = ? \]
- Idea: Disambiguate via the Principle of Maximum Entropy. (Ziebart, et al. 2008)
Principle Maximum Entropy Intuition
Key Idea: Don't commit to any particular prediction more than the data forces you too.
- Minimum Entropy Distribution: Assume agent's policy exactly matches the demonstrations.
- Maximum Entropy Distribution: Find distribution that matches measured moments, but has no additional bias.
- Examples:
- Uniform: [0, 1] domain and no moment matching constraints.
- Exponential: Positive reals domain and match expected value.
Boolean Rewards Intuition
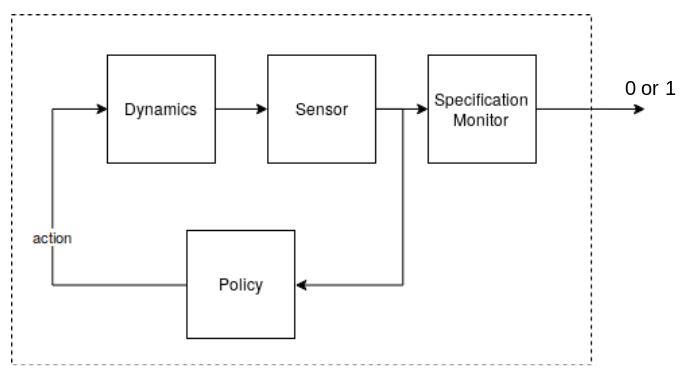
Boolean Rewards Intuition

Observe satisfaction probability, $p_\varphi$.
Boolean Rewards Intuition
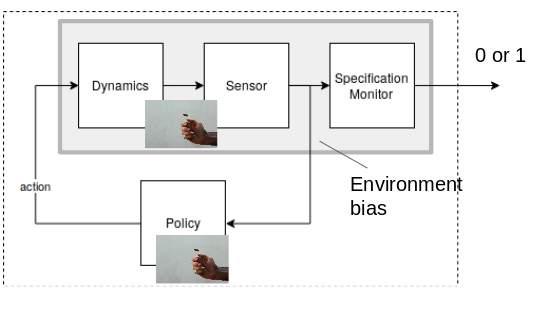
Satisfaction probability, $p_\varphi$, affected by policy and how "easy" the specification/dynamics combination is.
Boolean Rewards Max Ent Distribution
 \[
\begin{split}
&p_\varphi \triangleq \Pr(\xi \models \varphi~|~\text{teacher policy})\\
&q_\varphi \triangleq \Pr(\xi \models \varphi ~|~\text{random actions})
\end{split}
\]
\[
\begin{split}
&p_\varphi \triangleq \Pr(\xi \models \varphi~|~\text{teacher policy})\\
&q_\varphi \triangleq \Pr(\xi \models \varphi ~|~\text{random actions})
\end{split}
\]
- The Maximum Entropy Distribution given $p_\varphi$ is: \[ \Pr(s_{1:T} ~|~\text{demos}, \varphi) \propto \begin{cases} \frac{p_\varphi}{q_\varphi}& \text{if } s_{1:T} \in \varphi\\ \frac{p_{\neg \varphi}}{q_{\neg \varphi}}& \text{if } s_{1:T} \notin \varphi \end{cases} \]
- Note: When the dynamics are deterministic, this recovers the size principle from concept learning! (Tenenbaum 1999)
Maximum Entropy Likelihood given i.i.d. demos
Additional Assumptions
- Teacher at least as good as random: $p_\varphi \geq q_\varphi$
- Demonstrations, $\text{demos} = \{\xi_1, \xi_2, \xi_3, \ldots \xi_n \}$, given i.i.d.
- Demonstrations are representative: $p_\varphi \approx \frac{|\text{demos}~\cap~\varphi|}{n}$
- $P_\varphi \triangleq \text{coin with bias } p_\varphi ~~~~~Q_\varphi \triangleq \text{coin with bias } q_\varphi$
... Algebra ...
Aside: Can be interpreted as quantifying the atypicality of $\text{demos}$ over random action hypothesis.(Sanov's Theorem 1957)
Model Summary
$P_\varphi \triangleq \text{coin with bias } p_\varphi ~~~~~Q_\varphi \triangleq \text{coin with bias } q_\varphi$
\[ \Pr(\text{demos}~|~ \varphi) \propto 1[p_\varphi \geq q_\varphi]\exp{\Big(n\cdot D_{KL}(P_\varphi || Q_\varphi)\Big )} \]How to optimize?
\[ \Pr(\text{demos}~|~\varphi) \propto 1[p_\varphi \geq q_\varphi]\exp{\Big(n \cdot D_{KL}(P_\varphi || Q_\varphi)\Big )} \]- Suppose robot has a concept class, $\Phi$, of specifications.
- Want to make $p_\varphi$ and $q_\varphi$ as separate as possible.
- Gradients are not well defined: $p_{\varphi}$ and $q_{\varphi}$ change discretely.
Proposition 1:
\[ \varphi \subseteq \varphi' \implies \Big (p_{\varphi} \leq p_{\varphi}' \text{ and } q_{\varphi} \leq q_{\varphi}' \Big). \]
Monotonicity of Maximum Entropy Model
\[ \Pr(\text{demos}~|~\varphi) \propto 1[p_\varphi \geq q_\varphi]\exp{\Big(n\cdot D_{KL}(P_\varphi || Q_\varphi)\Big )} \]
Proposition 2:
The maximum entropy model above monotonically decreases in $q_\varphi$.
Monotonicity of Maximum Entropy Model
\[ f_i(x) \triangleq \Pr\left(\text{demos}~|~\varphi, p_\varphi = \frac{i}{n}, q_\varphi=x\right) \]Proposition 2:
The maximum entropy model above monotonically decreases in $q_\varphi$.
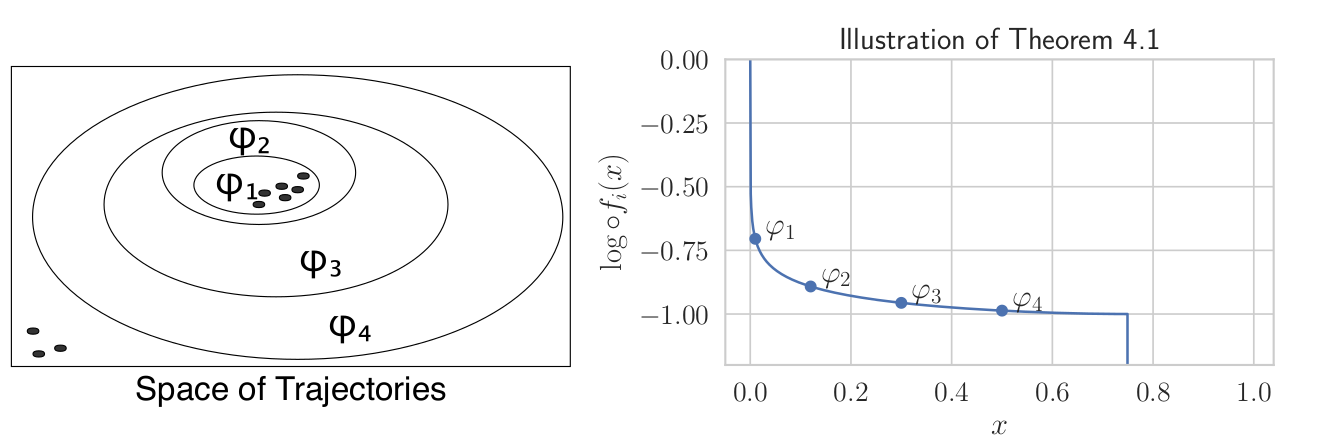
Caution - Can overfit

- Q: What is the likelihood of generating $\text{demos}$ given $\varphi = \text{demos}$?
- Mitigations:
- Constrain concept class, $\Phi \subsetneq S^\omega$. Examples: simple temporal logic formula, number of states in the automata, circuit complexity, etc.
- Carefully construct priors. Examples: exponential in description length, entropy, or circuit complexity.
- Avoid Maximum a Posteriori Estimation by marginalizing over the whole distribution.(reduction to $L^*$).
Preliminary Human Studies
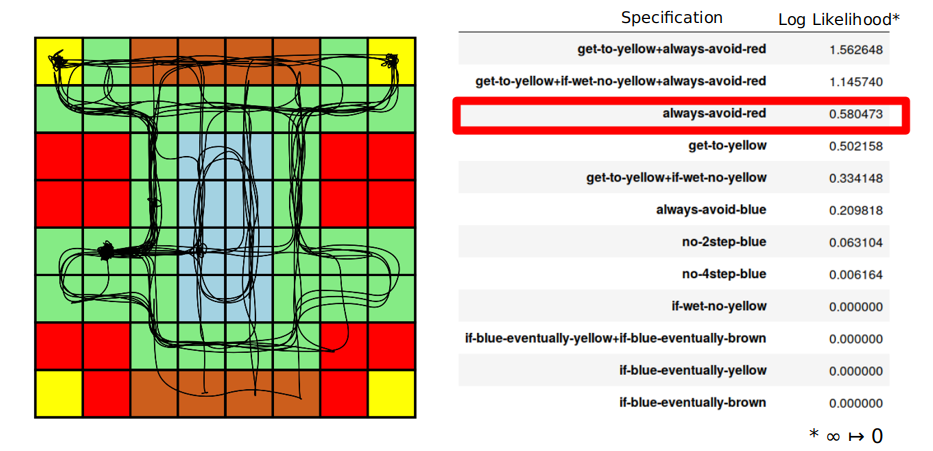
Structure of the talk
Prelude
Act 1 - Learning Specifications
- Formal Specification Propaganda
- Maximum Entropy Specification Learning (NeurIPS 2018, current work)
Act 2 - Teaching Specifications
- Episodic Specification Teaching (CPHS 2018, future work)
- Cooperative Planningfuture work
Act 3 - Challenge Problems
Human Understandable $\neq$ Machine Understandable
- Co-Op IRL / Showing vs Doing:
Teacher provides demonstrations that disambiguate objective (Hadfield-Menell et al 2016) (Ho et al 2016).
- Idea: Can these differences be explained by optimizing for our MaxEnt Specification Learner?
Teaching Problem Statement
- Assume the human performs Maximum Likelihood Estimation over a concept class $\Phi$ using a likelihood compatible with: \[ \Pr(\text{demos}~|~\varphi) \propto 1[p_\varphi \geq q_\varphi]\exp{\Big(n\cdot D_{KL}(P_\varphi || Q_\varphi)\Big )}. \]
- For a fixed $n \in \mathbb{N}$, find $n$ demonstrations that maximally disambiguate $\varphi^*$ from all other specifications in $\Phi$: \[ \max_{\text{demos}}\min_{\substack{\varphi \in \Phi\\\varphi \neq \varphi^*}}\Big(\Pr(\text{demos}~|~\varphi^*) - \Pr(\text{demos}~|~\varphi)\Big). \]
Select Demonstrations and World to Maximally Disambiguate
\[ \Pr(\text{demos}~|~\varphi) \propto 1[p_\varphi \geq q_\varphi]\exp{\Big(n\cdot D_{KL}(P_\varphi || Q_\varphi)\Big )} \]- Can control $p$ by changing the demonstrations.
- Can control $q$ by changing the world, e.g, the starting position.
Induced Ordering
Concept Class: $\Phi = \{\varphi^*, \varphi', \varphi''\}$
Structure of the talk
Prelude
Act 1 - Learning Specifications
- Formal Specification Propaganda
- Maximum Entropy Specification Learning (NeurIPS 2018, current work)
Act 2 - Teaching Specifications
- Episodic Specification Teaching (CPHS 2018, future work)
- Cooperative Planningfuture work
Act 3 - Challenge Problems
Communicating Trace Properties

- Proposal: Receding Horizon
Learning and Teaching for collaborative control.
- Infer objective, $\varphi_G$, of other agent based on their past actions.
- Objective 1 - Cooperation: Plan trajectory that helps the agent satisfy $\varphi_G$ (inspired by Liu et al., AAMAS 2016).
- Objective 2 - Information Gathering: Disambiguate other agent's objective. (inspired by Sadigh et al. IROS 2016)
- Apply first action of trajectory and replan.
A complete solution should also factor trajectory Legibility (Dragan et al 2013)
Act 3
Challenge Problems
Challenge Problems
-
Rental Car On-boarding
How to quickly communicate to new operatorfeatures and constraints (ODDs) of new vehicle, e.g, Tesla Autopilot. -
Joint drone control.

Drone with Human Operated ManipulatorPhoto: Energid -
Automated DMV crash report.

Uber Crash(Photo: FRESCO NEWS/Mark Beach)
Fin
Exploiting Binary Rewards
Exploiting Binary Rewards
Exploiting Binary Rewards
Exploiting Binary Rewards
Binary Decision Diagrams
Observation: Early "obviously correct" moves preferred.
Communicating Intent and Formal Specifications
- High level intent are specifications.
- Two types of intent: High level objective vs low level planning.
- Low level planning requires a dynamics model.
-
Did the agent intend to enter the lava?
-
Success probabilities induce an ordering.
Maximum Entropy Inverse Reinforcement Learning
\[\Pr(o_i = 1~|~s_i, a_i, r) \propto e^{r(s_i)}\]
- Idea: Disambiguate via the Principle of Maximum Entropy. (Ziebart, et al. 2008)(Cover and Thomas 2012)
- Can be derived using inference on above Graphical Model. (Levine 2018)
- Resulting distribution: \[ \Pr(s_{1:T}, a_{1:T}~|~o_{1:T}=1, r) \propto \Big( \prod_{i=1}^{T-1} \Pr(s_{i+1}~|~s_i, a_i)\Big) \Big( e^{\sum_{i=1}^T r(s_i, a_i))}\Big) \]
- Tune $r$ to match data, e.g, first moment of features.
Trace properties as Boolean Rewards
- Assume episode length $T \in \mathbb{N}$.
- Consider $\varphi$ decidable by time, $T \in \mathbb{N}$, e.g, $\varphi \subseteq S^T$.
- Define episode reward via $r_\varphi(s_{1:T}) = \mathbf{1}[s_{1:T} \in \varphi]$.
- Note: Made Markovian by unrolling Markov Decision Process.
-
Example: $\varphi(\xi) = $"Visit blue by t=2".
Trace properties as Boolean Rewards
- Maximum Entropy Distribution:
\[ \Pr(s_{1:T}, a_{1:T}~|~o_{1:T}=1, r) \propto \Big( \prod_{i=1}^{T-1} \Pr(s_{i+1}~|~s_i, a_i)\Big) \Big( e^{\sum_{i=1}^T r(s_i, a_i))}\Big) \]
- Maximum Entropy Distribution becomes:
\[ \Pr(s_{1:T}, a_{1:T}~|~o_{1:T}=1, \varphi) \propto e^{\lambda\cdot r_\varphi} \prod_{i=1}^{T-1} \Pr(s_{i+1}~|~s_i, a_i) \]
where $\lambda$ is tuned to match $\mathbb{E}_{s_{1:T}}(r_\varphi(s_{1:T})~|~\text{demos})$.
Note: Boolean rewards have only two values.
Bounded Trace properties as Boolean Rewards
- Maximum Entropy Distribution:
\[ \Pr(s_{1:T}, a_{1:T}~|~o_{1:T}, \varphi) \propto e^{\lambda\cdot r_\varphi} \prod_{i=1}^{T-1} \Pr(s_{i+1}~|~s_i, a_i) \]
- $W_\varphi \triangleq \sum_{s_{1:T} \in \varphi}\prod_{i=1}^T(\Pr(s_{i+1}~|~s_i, a_i))$.
- Two constraints:
\[ \begin{split} \text{Probabilities sum to 1: } &~~~~Z_\varphi = W_{\neg \varphi} e^0 + W_{\varphi} e^\lambda\\ \text{Feature Matching: }&~~~~Z_\varphi \mathbb{E}_{s_{1:T}}(r_\varphi(s_{1:T}~|~\text{demos})) = 1\cdot e^{\lambda}W_\varphi + 0\cdot e^{0} W_\varphi = e^{\lambda}W_\varphi \end{split} \]
Bounded Trace properties as Boolean Rewards
\[ \begin{split} &Z_\varphi = W_{\neg \varphi} e^0 + W_{\varphi} e^\lambda\\ &Z_\varphi \mathbb{E}_{s_{1:T}}(r_\varphi(s_{1:T})~|~\text{demos}) = e^{\lambda 1}W_\varphi\\\\ &p_\varphi \triangleq \mathbb{E}_{s_{1:T}}(r_\varphi(s_{1:T})~|~\text{demos})\\ &q_\varphi \triangleq \mathbb{E}_{s_{1:T}}(r_\varphi(s_{1:T})~|~\text{random actions}) = W_\varphi / Z_\varphi \end{split} \]
.... Algebra ...
Act 1.8
Post NeurIPS 2018
- Maximum A Posteriori $\to L^*$ Automata Learning
- Maximum Entropy $\to$ Maximum Causal Entropy
MAP considered Harmful
- Maximum a posteriori estimation throws away all of the distribution information.
MAP considered Harmful
- Maximum a posteriori estimation throws away all of the distribution information.
- Without proper priors this can lead to overfitting.
- Note: Marginalizing results in a "soft-decision": \[\Pr(\xi \in \varphi_*~|~\text{demos}) \propto \int_{\substack{\varphi \in \Phi\\\varphi\ni \xi}} \Pr(\xi~|~\text{demos}, \varphi)\Pr(\varphi).\]
- Set of $\kappa$-"probable" traces is a trace property. \[\varphi_\kappa \triangleq \Big\{\xi \in S^* ~.~\Pr(\xi \in \varphi_*~|~\text{demos}) > \kappa \Pr(\xi \notin \varphi_*~|~\text{demos})\Big\}\] where $\kappa \geq 1$.
Angluin Style Learning ($L^*$)
Learning Regular Languages (as DFAs) with minimally adequate teacher is polytime in the number of states. (Angluin 1987)
Minimally Adequate Teacher
- Membership$(\xi):$ Is $\xi$ a member of $\varphi_*$? (Y / N)
- Equivalence$(\varphi)$: Is $\varphi$ equivalent to $\varphi^*$? (Y / Counter Example)
Idea: Use $\kappa$ probable decision as membership oracle.
Benefits: Avoid overfitting + Learn outside of concept class.
Angluin Style Learning ($L^*$)
Learning Regular Languages (as DFAs) with minimally adequate teacher is polytime in the number of states. (Angluin 1987)
Proposed Teacher
- Membership($\xi$): $\Pr(\xi \in \varphi_*~|~\text{demos}) > \kappa \Pr(\xi \notin \varphi_*~|~\text{demos})$.
- NoisyEquivalence($\varphi$): Sample many $\xi_i$ and check if: \[\xi_i \in \varphi \iff \text{Membership}(\xi_i).\]
Maximum Entropy vs Maximum Causal Entropy
- Problem: $\Pr(s_{i+1}~|~s_i, a_i, o_i=1, r) \neq \Pr(s_{i+1}~|~s_i, a_i)$.
- Consequence: Agent implicitly assumes it has some control over dynamics.
\[ \Pr(s_{1:T}, a_{1:T}~|~o_{1:T}=1, r) \propto \Big( \prod_{i=1}^{T-1} \Pr(s_{i+1}~|~s_i, a_i)\Big) \Big( e^{\sum_{i=1}^T r(s_i, a_i))}\Big) \]
- Fix: Condition on causal information flow (Ziebart, et al. 2010, Levine 2018).
- Implication: $\pi(s_i~|a_i)$ Given via Soft Bellman Backup.
\[ \pi(a_i~|s_i) = \exp(Q(s_i, a_i) - V(s_i))\\ ~\\ Q(s_i, a_i) = r(s_i, a_i) + \mathbb{E}[V(s_{i+1})~|~s_i, a_i]\\ V(s_i) = \text{softMax}_{a\in A}(Q(s_i, a_i))\\ \]
Combinatorial Explosion!
Problem: How to do Bellman backup after unrolling?
Proposed Solution
- Model Markov Decision process as a probabilistic sequential circuit (SAT 2019 in submission)
- Represent tree via ordered Binary Decision Diagrams (Bryant 1992)
Legibility: Inference along the whole trajectory should be considered. (Dragan et al 2013).
Proposal: Use Maximum Causal Entropy BDD to select most legible demonstrations.
- Note: Shorter paths in BDD correlate to faster inference along path.
- "More obviously correct" actions have higher probability.
- Idea: Look for path that is comparatively short in objective's bdd.