Time-Series Learning using Monotonic Logical Properties

  • Marcell Vazquez-Chanlatte\(^{\star (\text{me})}\)
  • Shromona Ghosh\(^\star\)
  • Jyotirmoy V. Deshmukh\(^{\dagger}\)
  • Alberto Sangiovanni-Vincentelli\(^{\star}\)
  • Sanjit A. Seshia\(^\star\)

Slides @ mjvc.me/RV2018

\(\star\): University of California-Berkeley

\(\dagger\): University of Southern California

The Verification Problem

Specification Mining

An Incomplete Survery

Survey: Li, Wenchao. Specification mining: New formalisms, algorithms and applications.

$^1$Vazquez-Chanlatte et al, Logic-based Clustering and Learning for Time-Series Data, CAV 2017

$^2$ Bombara et al., Signal Clustering Using Temporal Logics, RV 2017.

Two Messages

Use Machine Learning to learn Formal Specifications.

Specification Mining

Use Formal Specifications to guide Machine Learning.

Logical Lens

This talk is about unifying these two.

Contributions

  1. Relax restrictions of our CAV 2017 work.
  2. Learn "traffic slow-down" spec from simple logical lens.

Logical Lens\(^*\) \[\downarrow\] Logic Respecting Distance
or
Features

\(^*\)Logical Lens = A Parametrized family of Boolean Properties, \(\phi : \text{Parameter} \to \big (\text{Data} \to \{0, 1\}\big )\), e.g. PSTL.

In memory of Oded Maler

  • Overlapped with my internship at Toyota.
  • Work on "Learning Monotone Partitions of Partially-Ordered Domains" was catalyst for this paper.

Outline

  1. Motivating Example
  2. Logical Lens \(\to\) Logical Distance

    Logical Lens \(\triangleq\) Parametric Trace Property

  3. Computing Logical Distance
  4. Application to Highway 101 data.

Motivating Example

Goal: Detect highway slow downs.

Have rough idea of shapes to look for.

Outline

  1. Motivating Example
  2. Logical Lens \(\to\) Logical Distance

    Logical Lens \(\triangleq\) Parametric Trace Property

  3. Computing Logical Distance
  4. Application to Highway 101 data.

Parametric Logical Formula

\[\phi(\tau, h) \triangleq \square_{[\tau, 20]}(\text{car_speed} \leq h)\]

Different parameters result in different classifications.

Platonic Ideal of a Metric

If two things are logically similar, they should be "close" together.

Platonic Ideal of a Metric

If two things are logically similar, they should be "close" together.

"If it quacks like a duck and looks like a duck\(\ldots \) it should have a small distance to a duck."

Domain Independent

Time-Series using PSTL is just an example

Logically Similar

Boolean Features

\[\varphi_i : \text{Data} \to \{0, 1\}\]

Each axis represents a property.

Families of Boolean features

  • Sometimes need to test $\geq 3$ properties.
  • Consider the following (infinite) size family of Boolean features.

You must be $h$ meters tall or more to ride.

Families of Boolean features

\[\phi : \text{Height} \to \bigg ( \text{Data} \to \{0, 1\}\bigg)\]

Families of Boolean features

\[\phi : \text{Data} \to \bigg ( \text{Height} \to \{0, 1\}\bigg)\]

Parametric Specifications

\[\phi : \text{Data} \to \bigg ( {[0, 1]}^n \to \{0, 1\}\bigg)\]

Data induces a geometric structure in the parameter space.

Monotonic Specifications

\[\phi : \text{Data} \to \bigg ( {[0, 1]}^n \to \{0, 1\}\bigg)\]

  1. Complicated geometry in general.
  2. Many families are "monotonic".

\[\theta \leq \theta' \implies \phi(x)(\theta) \leq \phi(x)(\theta')\]

Can Forget Interior

It is sufficent to just remember the boundary (surface)

Logical Lens

Map Data to Surfaces.

CAV 2017 work can only pick out a single point.

đŸ’°Billion Dollar QuestionđŸ’°

Does similar data induce a similar structure??

  1. Transform data into a surface encoding logical trade-offs.
  2. Does this transformation give us a metric that achieves our goals?

Platonic Ideal 2.0

"If it quacks like a duck and looks like a duck\(\ldots \) it should produce a similar validity domain boundary??"

Does similar data induce a similar structure??

It depends...

For many Monotonic Specifications this is true: \[ \big( x \geq \theta\big ) \text{ vs } \big(x + 0.1 \geq \theta\big) \]

Logical Distance Recipe

  1. Define logical lens: $\phi : \text{Data} \to \bigg ( {[0, 1]}^n \to \{0, 1\}\bigg)$
  2. Define distance metric between parameters.
  3. Lift parameter distance to distance between boundaries. (e.g., Hausdorff Distance)

Outline

  1. Motivating Example
  2. Logical Lens \(\to\) Logical Distance

    Logical Lens \(\triangleq\) Parametric Trace Property

  3. Computing Logical Distance
  4. Application to Highway 101 data.

Recursively Computing Boundaries

  2. Sample points from each rectangle.
  3. Compute Hausdorff Distance.

Technique due to Oded Maler.

Oded Maler. Learning Monotone Partitions of Partially-Ordered Domains 2017. ă€ˆhal-01556243〉

Recursively Computing Boundaries

Steady state error example

\(\Rightarrow \)

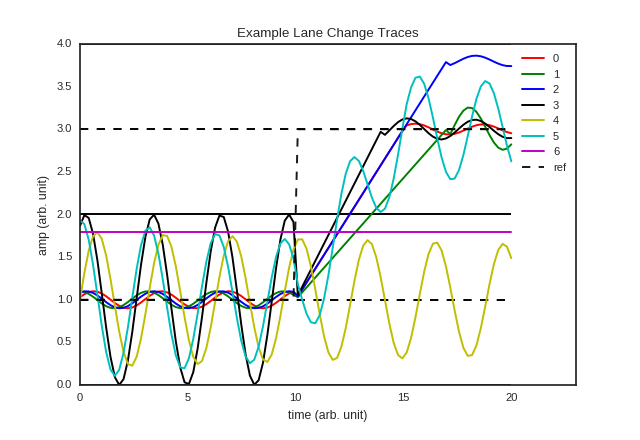
Slow Downs Revisited

\[\square_{[\tau, 20]}(\text{car_speed} \leq h) \]

Slow Downs Revisited

\[\square_{[\tau, 20]}(\text{car_speed} \leq h) \]

Outline

  1. Motivating Example
  2. Logical Lens \(\to\) Logical Distance

    Logical Lens \(\triangleq\) Parametric Trace Property

  3. Computing Logical Distance
  4. Application to Highway 101 data.

Real Highway Data Example

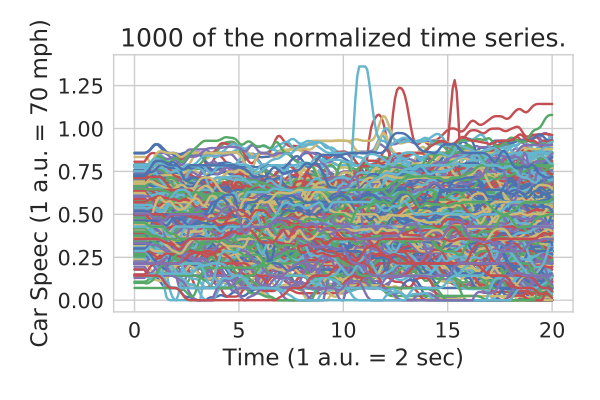
  • Want to detect traffic slow downs.
  • Too much data to run logical distance on!!!!
  • Many metric based learning algorithms are will require $O(\#\text{dataPoints}^2)$ queries.

Colyar, J., Halkias, J.: US highway 101 dataset. Federal Highway Administration (FHWA), Tech. Rep. FHWA-HRT-07-030 (2007)

Outline

  1. Motivating Example
  2. Logical Lens \(\to\) Coarse Logical Distance

  3. Computing Logical Distance
  4. Application to Highway 101 data.

Coarse Logical Features

Coarse Logical Features

Compute intersections along a line.

Coarse Logical Features

Parameterize line between 0 and 1.

\(\gamma_i : \text{Data} \to [0, 1]\).

Coarse Logical Features

Can project to multiple lines.

Outline

  1. Motivating Example
  2. Logical Lens \(\to\) Logical Distance

    Logical Lens \(\triangleq\) Parametric Trace Property

  3. Computing Logical Distance
  4. Application to Highway 101 data.

Real Highway Data Example

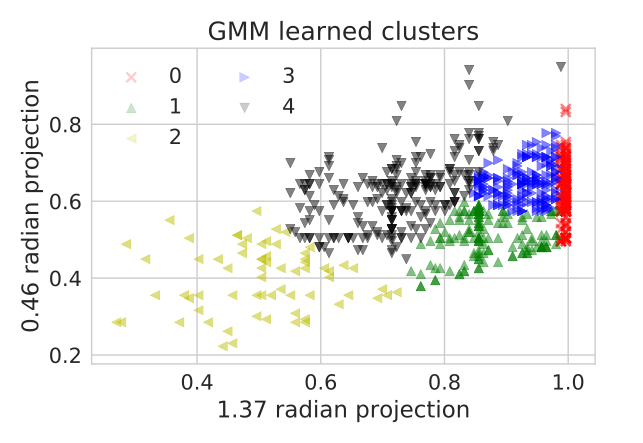
  1. Project onto two interior lines.
  2. Label using Gaussian Mixture Model.
  3. Label toy data to identify possible slow downs.

Distance to Idealized Slowdown

Zoom in on cluster 4 by computing distances to idealized slow down.

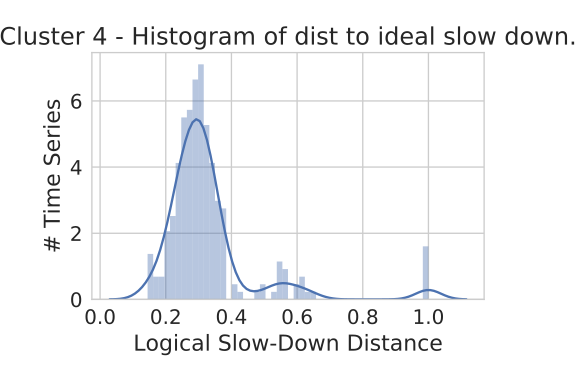
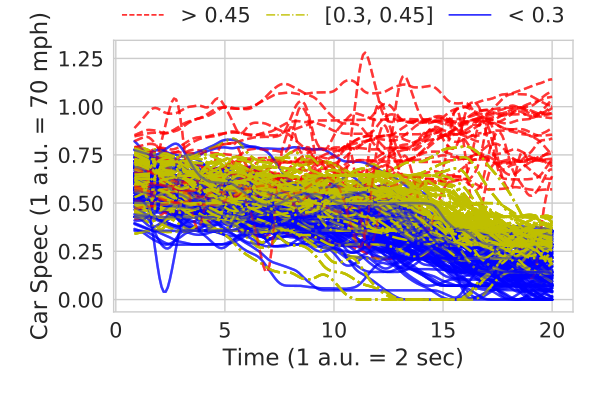
Extract Formula?

Labels \(\to\) Parameter Ranges \(\to\) Formula

Details in the CAV 2017 paper.

Logic-based Clustering and Learning for Time-Series Data, CAV 2017

Slow Down Formula

Extracting a formula:

\[ \phi(\tau, h) \triangleq \square_{[\tau, 20]}(\text{car_speed} < h) \]

\[ \psi_1 = \phi(0.25, 0.55) \wedge \neg \phi(0.38, 0.55) \wedge \neg \phi(0.25, 0.76) \]

\[ \psi_2 = \phi(0.35, 0.17) \wedge \neg \phi(0.35, 0.31) \wedge \neg \phi(0.62, 0.17) \]

\[\text{slow_down} \triangleq \psi_1 \wedge \psi_2\]

Two Messages

Use Machine Learning to learn Formal Specifications.

Specification Mining

Use Formal Specifications to guide Machine Learning.

Logical Lens

Summary

  1. Relax restrictions of our CAV 2017 work.
  2. Learn "traffic slow-down" spec from simple logical lens.

Logical Lens\(^*\) \[\downarrow\] Logic Respecting Distance
or
Features

Future work

  1. Performance improvements.
  2. Kernel trick analog to learn better specifications.

Questions?

Slides @ mjvc.me/RV2018

Code @ github.com/mvcisback/multidim-threshold

A hammer looking for a nail?

  1. A lot of great tools to time-series learning: Dynamic Time Warping, Shaplets, PCA, ...
  2. All of these techniques are fantastic!
  3. But you know what's better? A good feature.

Feature Engineering is King

"Coming up with features is difficult, time-consuming, requires expert knowledge. "Applied machine learning" is basically feature engineering."

- Andrew Ng,
"Machine Learning and AI via Brain simulations"

" …some machine learning projects succeed and some fail. What makes the difference? Easily the most important factor is the features used."

- Pedro Domingos,
"A Few Useful Things to Know about Machine Learning"

... or at least is was before Deep Learning

Designing features is HARD

  1. Need to embed non-trivial domain specific knowledge into the feature.
  2. Domain specific knowledge is typically stuck in the head of a non-ML expert.
  3. ML techniques can be sensitive to encoding of features.

This work focuses on try to make designing features slightly less hard (e.g., time series).

Validity Domain

\[\phi : \text{Data} \to \bigg ( {[0, 1]}^n \to \{0, 1\}\bigg)\]

\[V_\phi(x) \triangleq ~\text{preImg}_{\phi(x)}[\{1\}] = \{\theta \in {[0, 1]}^n~.~\phi(x)(\theta) = 1\}\]

What's to come

(3/5) Derive a "logical distance" under this lens.

\[\phi(\tau, h) \triangleq \square_{[\tau, 20]}(\text{car_speed} \leq h)\]

What's to come

(4/5) Apply to real highway data.

\[\phi(\tau, h) \triangleq \square_{[\tau, 20]}(\text{car_speed} \leq h)\]

What's to come

(5/5) Characterize slow downs in this dataset.

\[\phi(\tau, h) \triangleq \square_{[\tau, 20]}(\text{car_speed} \leq h)\]

\[ \begin{split}\psi_1 \triangleq \phi(0.25, 0.55) &\wedge \neg \phi(0.38, 0.55) \\&\wedge \neg \phi(0.25, 0.76)\end{split} \]

\[ \begin{split}\psi_2 \triangleq \phi(0.35, 0.17) &\wedge \neg \phi(0.35, 0.31) \\&\wedge \neg \phi(0.62, 0.17)\end{split} \]

\[\text{slow_down} \triangleq \psi_1 \wedge \psi_2\]

Distance between Parameters

Infinity Norm: Let the distance between two parameters be the difference in their largest component, e.g,

\[ \text{height} \mapsto h, \text{weight} \mapsto w \] \[ d_\infty((h_1, w_1), (h_2, w_2)) \triangleq \max(|h_1 - h_2|, |w_1 - w_2|)\]

Distance between Boundaries

Hausdorff Distance: Let $A$ and $B$ be two sets of parameters:

\[ d^H_\infty(A, B) \triangleq \max(\sup_{a \in A} \inf_{b \in B} d_\infty(a, b), \sup_{b \in B} \inf_{a \in A} d_\infty(a, b))\]

Distance between Boundaries

\[ d^H_\infty(A, B) \triangleq \max(\sup_{a \in A} \inf_{b \in B} d_\infty(a, b), \sup_{b \in B} \inf_{a \in A} d_\infty(a, b))\]

Interpretation: The curves "\(\epsilon\)-bisimulate" each other.

  1. Two player game where player 1 selects a point, $a \in A$ and then player 2 selects a point $b\in B$.
  2. Player 1 wants to maximize distance between and $a$ and $b$.
  3. Player 2 wants to minimize the distance.
  4. They then switch roles.